高等教育出版社《电路原理》温习札记
电路理论是一门研究电路分析与网络综合,以及设计规律的基础工程学科。所谓电路分析就是指在给定的电路参数条件下,通过求解电路当中的电压、电流了解其所具有的特性;而网络综合是在给定电路技术指标的情况下,设计出电路并且确定元件的参数,使得电路的性能符合预先的设计要求。因此电路分析是电路理论当中最为基础的内容,也是学习电路理论的入门课程,更被列为电子信息工程类专业的通用基础课,因而其重要地位不言而喻。

电路理论作为电子信息工程类专业的技术基础课,可以为相关专业的后续诸多课程提供理论支持,例如模拟电子技术、数字电子技术、信号与系统、电机学、电力系统分析、集成电路设计、自动控制、电力电子技术等课程,它们都需要应用到电路理论当中的相关基础知识。
电路模型与电路定律
电路与电路模型
电路 (Circuit) 也被称为网络 (Network),其中电能或者电信号的发生装置称为电源,而用电设备则被称为负载。
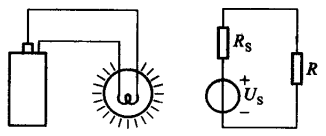
- 激励:是指在电路当中产生
电压、电流的电源; - 响应:是指由于激励而在电路当中产生的
电压与电流;
注意:根据激励与响应之间的因果关系,可以将激励称为输入,而响应称为输出。
注意:集总参数元件假定是指任意时刻流入二端元件某一个端子的电流,一定等于从另外一个端子流出的电流,并且两个端子之间的电压为一个单值量。由集总参数元件构成的电路被称为集总参数电路。
注意:如果表征元件特性的代数关系是线性关系,则称该元件称为线性元件。如果这种代数关系属于非线性关系,则称该元件被称作非线性元件。
电流 & 电压的参考方向
电路理论当中涉及的物理量主要有电流 \(I\)、电压 \(V\)、电荷 \(Q\)、磁通 \(\varPhi\)
[faɪ]、磁通链 \(\varPsi\)
[psaɪ]、电功率 \(P\)、电能 \(W\)。
当分析某一个元件或者某一部分电路的电流或者电压时,由于两者的实际方向未知,需要为其指定一个参考方向,从而可以将电压或者电流视为代数量来进行处理。
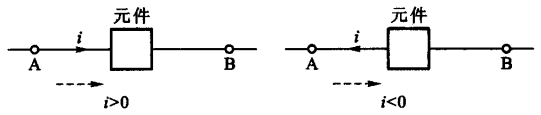
如果电流的参考方向与实际方向一致,则电流为正值(\(i>0\)),否则就为负值(\(i<0\))。电流的参考方向可以任意指定,一般使用箭头和双下标来进行表示。
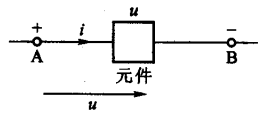
电压的参考方向也称为参考极性,表达两点之间的电压时,使用正极性
+ 表示高电位,而负极性
-
表示低电位,由正极指向负极的方向就是电压的参考方向。
注意:当电路中的电流、电压、电荷等变量随时间变化时,通常约定使用小写字母
i、u、q进行表示,而使用大写字母I、U、Q表示较为恒定的变量,具体的命名还需要结合上下文进行分析。
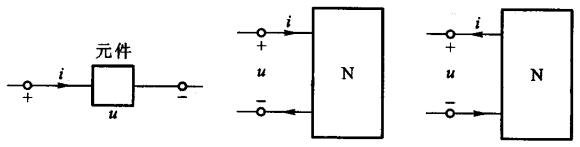
电流或者电压的参考方向可以独立的进行指定,如果电流与电压的参考方向一致,就称为关联参考方向,否则就称为非关联参考方向(下面第
1、2 图为关联参考方向,而 第 3 图属于非关联参考方向):
国际单位制(SI,International
System of
Units)当中,电流的单位为安培
A(简称安),电荷的单位为库仑
C(简称库),电压的单位为伏特
V(简称伏),这些单位可以与如下表示数量级的词头叠加使用:
| 中文词头 | 英文前缀 | 英文缩写 | 进制 | 中文词头 | 英文前缀 | 英文缩写 | 进制 |
|---|---|---|---|---|---|---|---|
| 尧 | Yotta |
Y | \(10^{24}\) | 分 | deci |
d | \(10^{-1}\) |
| 泽 | Zetta |
Z | \(10^{21}\) | 厘 | centi |
c | \(10^{-2}\) |
| 艾 | Exa |
E | \(10^{18}\) | 毫 | milli |
m | \(10^{-3}\) |
| 拍 | Peta |
P | \(10^{15}\) | 微 | micro |
μ | \(10^{-6}\) |
| 太 | Tera |
T | \(10^{12}\) | 纳 | nano |
n | \(10^{-9}\) |
| 吉 | Giga |
G | \(10^{9}\) | 皮 | pico |
p | \(10^{-12}\) |
| 兆 | Mega |
M | \(10^{6}\) | 飞 | femto |
f | \(10^{-15}\) |
| 千 | kilo |
k | \(10^{3}\) | 阿 | atto |
a | \(10^{-18}\) |
| 百 | hecta |
h | \(10^{2}\) | 仄 | zepto |
z | \(10^{-21}\) |
| 十 | deca |
da | \(10^{1}\) | 幺 | yocto |
y | \(10^{-24}\) |
电功率 & 能量
电功率与电压和电流密切相关,当正电荷从元件上面电压的正极,经过元件运动至电压的负极时,与该电压相对应的电场力需要对电荷作正功,此时元件吸收能量;反之,正电荷从电压的负极,经过元件运动到电压的正极时,与该电压相对应的电场力作负功,元件向外释放电能。
电压的定义是指 A 与 B
两点的电压等于电场力将单位正电荷从 A
点移动至 B 点时所作的功。如果在 \(dt\) 时间之内,存在着 \(dq\)
电荷从元件电压的正极,经过电压 \(u\)
到达电压的负极,此时电场力所做的功,即元件吸收的能量
\(W\) 等于:
\[ dW = udq \]
此时假设元件上的电流 i
与电压 u 成关联参考方向,根据电流
i 的定义 \(i =
\frac{dq}{dt}\) 可以推导得到 \(dW =
uidt\),由于功率 p 是能量 W
的导数,所以元件吸收的功率 \(p\) 等于:
\[ p = \frac{dW}{dt} = ui \]
- 当电压 \(u\) 与电流 \(i\) 处于关联参考方向时,功率 \(p = ui\) 为正值表示该元件吸收功率,反之亦然;
- 当电压 \(u\) 与电流 \(i\) 处于非关联参考方向时,功率 \(p = ui\) 为正值表示该元件发出功率,反之亦然;
此时在 \(t_0\) 到 \(t\) 的时间范围以内,该元件吸收的能量 \(W\) 等于:
\[ W(t) = \int dW = \int^{q(t)}_{q(t_0)} udq = \int^{t}_{t_0} u(\xi) i(\xi) d \xi \]
注意:能量 \(W\) 的单位为焦耳
J(简称焦),功率 \(p\) 的单位为瓦特W(简称瓦)。
电阻元件
当线性电阻元件的电压与电流取关联参考方向时,任意时刻其两端的电压
u 与电流 i
都遵守欧姆定律:
\[ u = Ri \]
上面等式当中的 R 称为元件的电阻,当电压
u 的单位采用伏特,而电流 i
的单位采用安培时,电阻的单位为欧姆
Ω,简称为欧。线性电阻元件的符号如下图所示:
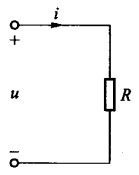
电阻的电导 \(G =
\frac{1}{R}\),其单位为西门子
S,简称为西,此时就可以把欧姆定律转换为下面形式:
\[ i = Gu \]
注意:如果电压
u与电流i的参考方向取非关联参考方向,那么 \(u = - Ri\) 并且 \(i = - Gu\)。
由于电压的单位为伏,而电流的单位为安,因而电阻元件的特性也被称为伏安特性。下图是一个线性电阻元件的伏安特性曲线,它是一条通过原点的直线,其斜率与元件的电阻
R 相关:
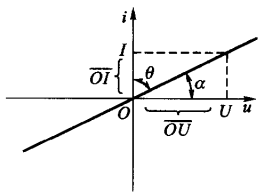
当一个线性电阻元件两端的电压无论为何值时,经过的电流恒为零,这种现象称为开路。其伏安特性曲线与电压
u 轴重合,也即相当于 \(R=\infty\),\(G=0\):
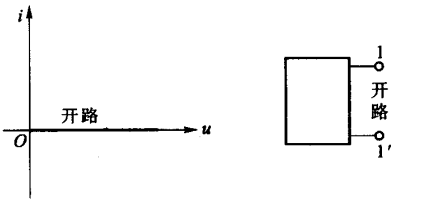
当流过一个线性电阻元件的电流无论为何值时,其两端的电压恒为零,这种现象称为短路。其伏安特性曲线与电流
i 轴重合,即相当于 \(R=0\),\(G=\infty\):
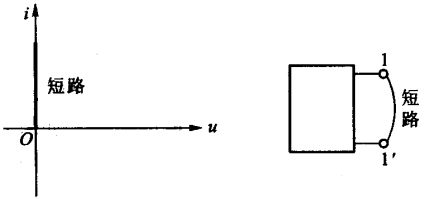
当电压 \(u\) 与电流 \(i\) 取关联参考方向时,电阻元件消耗的功率 \(p\) 等于:
\[ \begin{aligned} p = ui = R i^2 = \frac{u^2}{R}\\ = G u^2 = \frac{i^2}{G} \end{aligned} \]
电阻元件从 \(t_0\) 到 \(t\) 的时间之内,所吸收的能量 \(W\) 等于:
\[ W = \int^{t}_{t_0} R i^2 (\xi) d \xi \]
注意:电阻元件一般会将吸收的电能转换成热能或者其它形式的能量。
非线性电阻元件的伏安特性曲线并非一条通过原点的直线,其电压电流关系通常可以写作:
\[ u = f(i)\ 或者\ i = h(u) \]
时变电阻元件的电压 u
与电流 i
呈比例关系,但是比例系数 R
会随着时间 t 进行变化:
\[ u(t) = R(t) \cdot i(t)\ 或者\ i(t) = G(t) \cdot u(t) \]
注意:通常情况下,线性电阻元件的伏安特性曲线位于第
1、3象限,而负电阻元件的伏安特性曲线位于第2、4象限,其电阻值为负值 \(R < 0\),本质上就是一个发出电能的元件。
电压源与电流源
电压源和电流源都是从实际电源抽象而来的电路模型,属于二端有源元件。
电压源
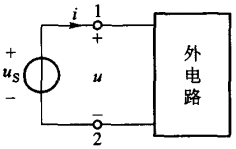
电压源是一个理想电路元件,其端电压 \(u(t) = u_s(t)\)。其中 \(u_s(t)\) 为给定的时间函数,称为电压源的激励电压。电压源的电压 \(u(t)\) 与通过元件的电流无关,总保持为给定的时间函数,而电流的大小则由外电路决定。电压源的符号如下图所示:
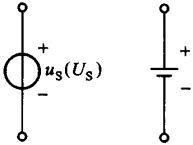
当电压源接入外电路时,端子
1 与 2 之间的电压 \(u(t)\) 等于 \(u_s(t)\),并且不会受到外电路的影响。
下图是电压源在 \(t_1\)
时刻的伏安特性曲线,这是一条不通过原点,并且与电流 i
轴平行的直线。当 \(u_s(t)\)
随着时间改变的时候,这条直线的位置会随之进行平移:
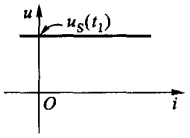
当 \(u_s(t)\) 为恒定值的时候称为直流电压源,通常使用 \(U_S\) 表示。下图是其伏安特性曲线,该直线的位置不会随着时间进行变化:
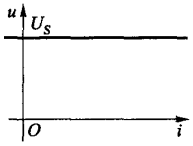
- 如果电压源不连接到外电路,那么电流总是为零值,这种情况称为电压源处于开路状态。
- 如果电压源的电压 \(u_s =
0\),则该电压源的伏安特性曲线与电流
i轴重合,称该电压源处于短路状态;将电压源短路没有任何意义,因为短路时的端电压 \(u = 0\),这与电压源的特性并不相符;
电流源
电流源同样是一个理想电路元件,其输出的电流 \(i(t) = i_s(t)\)。其中 \(i_s(t)\) 为给定的时间函数,称为电流源的激励电流。电流源的电流 \(i(t)\) 与通过元件的端电压无关,总保持为给定的时间函数,而端电压的大小则由外电路来决定。电流源的符号如下图所示:
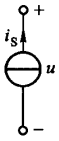
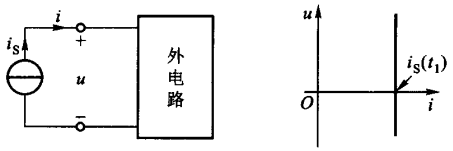
当电流源接入外电路时,电流源在
\(t_1\)
时刻的伏安特性曲线,是一条不通过原点,并且与电压 u
轴平行的直线。当 \(i_s(t)\)
随着时间变化时,该直线的位置将会随之进行平移:
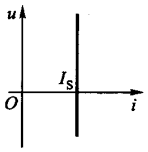
当 \(i_s(t)\)
为恒定值的时候就称为直流电流源,通常使用 \(I_S\)
进行表示。下图是其伏安特性曲线,该直线的位置不会随着时间 t
进行变化:
正弦电压源 & 正弦电流源
当电压源的电压 \(u_s(t)\)
或者电流源的电流 \(i_s(t)\) 随着时间 t
进行正弦周期性变化时,就可以称两者为正弦电压源或者正弦电流源。
假设 \(U_m\)
为正弦电压的最大值,\(T\) 为正弦函数的周期,而
\(f = \frac{1}{T}\)
为其频率(单位为赫兹
Hz), \(\omega = 2 \pi f\)
为角频率,\(\phi\)
为正弦函数的初相角,则该正弦电压可以被表达为下面几种形式:
\[ \begin{aligned} u_s(t) &= U_m \cos (\frac{2\pi}{T}t + \phi) \\ &= U_m \cos (2\pi ft + \phi) \\ &= U_m \cos (\omega t + \phi) \\ \end{aligned} \]
注意:独立源所谓的独立,是相对于后续即将介绍的受控源而言的。
受控电源
受控电源也称为非独立电源,其激励电压或者激励电流会受到电路当中某部分电压或者电流的控制。例如双极性晶体管的集电极电流会受到基极电流的控制,而运算放大器的输出电压会受到输入电压的控制。根据受控电压源或受控电流源的控制量是电压还是电流,可以将其具体划分为如下四种:
- 电压控制电压源(VCVS,Voltage Controlled Voltage Source);
- 电压控制电流源(VCCS,Voltage Controlled Current Source);
- 电流控制电压源(CCVS,Current Controlled Voltage Source);
- 电流控制电流源(CCCS,Current Controlled Current Source);
这四种受控源的符号分别如下图所示,图中的菱形符号表示电源部分,而
\(u_1\) 和 \(i_1\)
分别表示控制电压与控制电流,\(u\)、\(r\)、\(g\)、\(\beta\)
分别是相关的控制系数(其中 r
具有电阻量纲,而 g 具有电导量纲):

当控制系数 \(u\)、\(r\)、\(g\)、\(\beta\) 是一个常数的时候,被控制量与控制量就会呈正比,这种受控源被称为线性受控源。
- 独立源:表示的是外界对于电路的作用效果,电路当中的
电压/电流是由于独立电源起到的激励作用而产生; - 受控源:用于反映电路当中某一处的
电压/电流能够控制另外一处的电压/电流,或者表示某一个电路变量与另外一个电路变量之间的耦合关系;
注意:当求解具有受控源的电路时,可以把受控
电压/电流源作为普通的电压/电流源来进行处理,但是其激励电压/电流取决于控制量。
基尔霍夫定律
在介绍基尔霍夫定律之前,需要首先介绍一下支路、结点、回路的概念:
- 支路:组成电路的每一个二端元件;
- 结点:每一条支路之间的连接点;
- 回路:由支路构成的闭合路径;
如果将电路当中各条支路的电流与电压(简称支路电流与支路电压)作为变量来看待,那么这些变量总是会受到下面两类约束:
- 由元件自身特性造成的约束,例如线性电阻元件的电压与电流必须满足 \(u = Ri\),称为电压电流关系(VCR,Voltage Current Relation);
- 元件相互连接之后,给支路电流或者电压带来的约束关系,也称为几何约束或者拓扑约束,这类约束由基尔霍夫定律进行体现,其主要内容包括有 电流定律 KCL 和电压定律 KVL;
基尔霍夫电流定律
基尔霍夫电流定律(KCL,Kirchhoff's Current Law)是指在集总参数电路当中,在任意时刻对于任意一个结点,所有流出该结点的支路电流的代数和恒等于零,即对于任意结点都有 \(\Sigma i = 0\)。该定律通常应用于结点,对于包含有几个结点的闭合面同样适用。
注意:如果流出结点的电流取正
+,那么流入结点的电流就取负-,这里的流入与流出都需要根据电流的参考方向进行判断。
基尔霍夫电压定律
基尔霍夫电压定律(KCL,Kirchhoff's Voltage Law)是指在集总参数电路当中,在任意时刻沿着任意一条回路,所有支路电压的代数和恒等于零,即对于任意回路都有 \(\Sigma u = 0\)。
注意:如果支路电压的参考方向与回路绕行方向一致,则该电压取 正
+;如果支路电压的参考方向与回路绕行方向相反,则该电压取负-。
电阻电路的等效变换
- 由
时不变线性无源元件、线性受控源、独立电源组成的电路,称为时不变线性电路(简称线性电路); - 如果构成电路的无源元件均为
线性电阻,则称该电路为线性电阻性电路(简称电阻电路); - 当电路中的独立电源都使用
直流电源,这类电路就简称为直流电路;
电路分析计算时,可以对电路当中的某一部分进行简化,从而使用一个比较简单的电路进行代替,这个过程称为电路的等效变换。例如下图左右两个电路当中,端子
1 和 1' 具有相同的伏安特性,则右侧电路的 \(R_{eq}\)
就被称为等效电阻,其值取决于原电路当中各个电阻的值及其连接关系:

注意:使用等效电路求解分析电路的时候,
电压和电流保持不变的部分仅限于等效电路以外,也就是外部特性等效,即对外等效,而该电路内部并非是等效的。
电阻的串联
当 \(R_1,R_2 ... R_n\) 共
n
个电阻进行串联时,通过每一个电阻的电流相等。
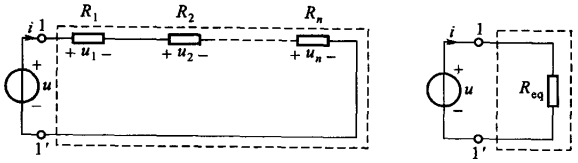
根据上面的电路,可以列写出 KVL 方程 \(u = u_1 + u_2 + ...
u_n\)。由于通过每一个电阻的电流均为 i,则可以得到
\(u_1 = R_1 i\)、\(u_2 = R_2 i\)、\(u_n = R_n i\),将它们代入
KVL 方程则可以继续得到 \(u =
(R_1 + R_2 + ... + R_n) i = R_{eq}
i\),此时等效电阻 \(R_{eq} = R_1 + R_2 + ... R_n = \sum^{n}_{k=1}
R_k\),具体的推导步骤如下面所示:
\[ \begin{cases} u_1 = R_1 i \\ u_2 = R_2 i \\ ...\ ...\ ...\ ... \\ u_n = R_n i \\ u = u_1 + u_2 + ... u_n \end{cases} \implies u = (R_1 + R_2 + ... + R_n) i = R_{eq} i \implies R_{eq} = R_1 + R_2 + ... R_n = \sum^{n}_{k=1} R_k \]
注意:串联电阻电路的等效电阻 \(R_{eq}\) 必然大于任意一个单独的串联电阻。
当 n
个电阻相互串联时,每一个电阻上面的电压都可以利用下面的分压公式计算得到:
\[ u_n = R_n i = \frac{R_n}{R_{eq}} u \]
电阻的并联
当 \(R_1,R_2 ... R_n\) 共
n
个电阻进行并联时,每一个电阻两端的电压相等。
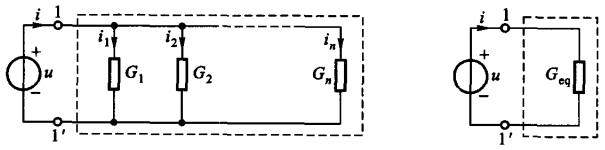
根据上面的电路,可以列写出 KCL 方程 \(i = i_1 + i_2 + ...
i_n\)。由于每一个电阻两端的电压均为 u,则可以得到
\(i_1 = G_1 u\)、\(i_2 = G_2 u\)、\(i_n = G_n u\),将它们代入
KCL 方程就可以继续得到 \(i =
(G_1 + G_2 + ... + G_n) u = G_{eq}
u\),此时并联之后的等效电导 \(G_{eq} = G_1 + G_2 + ... G_n = \sum^{n}_{k=1}
G_k\),而并联之后的等效电阻 \(R_{eq} = \frac{1}{G_{eq}} = \frac{1}{\sum_{k=1}^n
G_k} = \frac{1}{\sum_{k=1}^n
\frac{1}{R_k}}\),从而可以发现等效电阻小于每一个并联电阻,具体的推导步骤如下面所示:
\[ \begin{cases} i_1 = G_1 u \\ i_2 = G_2 u \\ ...\ ...\ ...\ ... \\ i_n = G_n u \\ i = i_1 + i_2 + ... i_n \end{cases} \implies i = (G_1 + G_2 + ... + G_n) u = G_{eq} u \implies G_{eq} = G_1 + G_2 + ... G_n = \sum^{n}_{k=1} G_k \implies R_{eq} = \frac{1}{G_{eq}} = \frac{1}{\sum_{k=1}^n G_k} = \frac{1}{\sum_{k=1}^n \frac{1}{R_k}} \]
注意:并联电阻电路的等效电阻 \(R_{eq}\) 必然小于任意一个单独的并联电阻。
当 n
个电阻相互并联时,通过每一个电阻的电流都可以利用下面的分流公式进行计算:
\[ i_n = G_n u = \frac{G_n}{G_{eq}} i \]
有一种特殊情况是,如果并联电阻的数量
n = 2,即两个电阻并联在一起,则其等效电阻
\(R_{eq}\)
可以采用如下更为便捷直观的计算方式:
\[ R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} = \frac{R_1 R_2}{R_1 + R_2} \]
电阻的 \(Y - \Delta\) 等效变换
电阻除了串并联之外,还存在着一种特殊的连接形式,即下图所示的桥形连接。此时无法根据电阻的串并联关系,对电路进行简化:
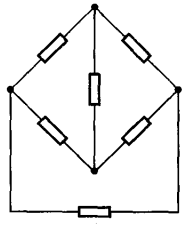
如果在该电路的任意一条支路上,加入一个电压源,就可以得到一个惠斯通电桥电路,其中 \(R_1\)、\(R_2\)、\(R_3\)、\(R_4\) 所在支路称为桥臂,而 \(R_5\) 所在的支路称为对角线支路:
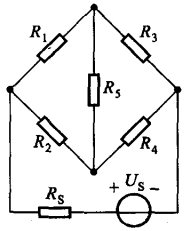
不难证明,当满足条件 \(R_1 R_4 = R_2 R_3\) 时,对角线支路上的电流为零,称为电桥处于平衡状态,这个条件也被称为电桥的平衡条件。当电桥平衡时 \(R_5\) 可以视为开路或者短路,此时电路可以按照串并联规律进行计算。但是当电桥不满足平衡条件时,就无法运用串并联关系进行计算,而需要用到接下来介绍的 \(Y - \Delta\) 等效变换。其中 \(Y\) 形联结也称为星形联结(下图左),而 \(\Delta\) 形联结也称为三角形联结(下图右),它们都通过 3 个端子与外部进行连接:
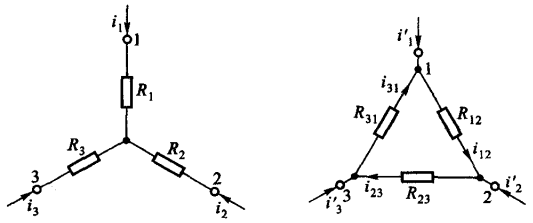
当两个电路的电阻之间满足一定关系时,它们在端子
1、2、3
上面的外特性就可以相同,此时它们相互之间可以进行等效变换。\(Y - \Delta\)
等效变换的条件是对应的端子之间具有相同电压 \(u_{12}\)、\(u_{23}\)、\(u_{31}\),而流入对应端子的电流全部相等
\(i_1 = i_1'\)、\(i_2 = i_2'\)、\(i_3 = i_3'\)。
下面展示了如何根据 \(\Delta\) 形联结的电阻,进而确定 \(Y\) 形联结电阻的公式及其相应的归纳形式:
\[ \begin{cases} R_1 = \frac{R_{12} R_{31}}{R_{12} + R_{23} + R_{31}}\\ R_2 = \frac{R_{23} R_{12}}{R_{12} + R_{23} + R_{31}}\\ R_3 = \frac{R_{31} R_{23}}{R_{12} + R_{23} + R_{31}} \end{cases} \implies \begin{cases} Y 形电阻 = \frac{\Delta 形相邻电阻的乘积}{\Delta 形电阻之和} \\ \Delta 形电阻 = \frac{Y 形电阻两两乘积之和}{Y 形不相邻电阻} \end{cases} \]
如果 \(Y\) 形联结当中的 3 个电阻相等,即 \(R_1 = R_2 = R_3 = R_Y\);那么其对应等效 \(\Delta\) 形联结当中的 3 个电阻也相等,即 \(R_{\Delta} = R_{12} = R_{23} = R_{31} = 3R_Y\),这个规律同样可以归纳为下面的形式:
\[ R_Y = \frac{1}{3} R_{\Delta} \]
电压源的串联
n
个电压源的串联,可以被等效替代为一个电压源:

这个等效电压源的激励电压 \(u_S\) 可以通过下面的公式进行计算(如果
\(u_{Sk}\) 的参考方向与 \(u_S\) 的参考方向一致,则 \(u_{Sk}\) 的前面取 +
正号,否则就取 - 负号):
\[ u_S = u_{S1} + u_{S2} + ... + u_{Sn} = \sum_{k=1}^n u_{Sk} \]
注意:只有激励电压相等,并且极性一致的电压源才允许并联,否则违背 KVL 定律。其等效电路为其中任意一个电压源,但是电压源并联之后向外提供的电流,以及各个电压源之间如何分配这些电流是无法确定的。
电流源的并联
n
个电流源的并联,也可以被等效替代为一个电流源:
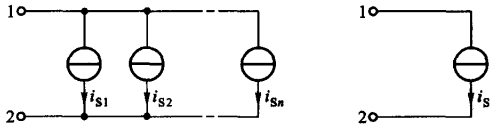
这个等效电流源的激励电流 \(i_S\) 也可以通过下面的公式进行计算(如果
\(i_{Sk}\) 的参考方向与 \(i_S\) 的参考方向一致,则 \(i_{Sk}\) 的前面取 +
正号,否则就取 - 负号):
\[ i_S = i_{S1} + i_{S2} + ... + i_{Sn} = \sum_{k=1}^n i_{Sk} \]
注意:只有激励电流相等,并且方向一致的电流源才允许串联,否则违背 KCL 定律。其等效电路为其中任意一个电流源,但是电流源串联之后总电压,以及该总电压如何在各个电流源之间分配则无法确定。
实际电源模型及其等效变换
下图左侧是一个实际的直流电源(例如电池),而右侧则是其输出电压
u 与输出电流 i
的伏安特性曲线。观察可以看到电压 u 随着电流 i
的增大而减少(它们并未构成线性关系):

此时电流 i
不能超过限定的值,否则将会导致电源的损坏。但是在某一个范围以内,可以将电压与电流的关系近似为直线,如果把这一段直线加以延长,作为该电源的外特性曲线,如下图所示:

观察就可以发现,这个外特性曲线在 u 轴和 i
轴上各有一个交点,其中 \(U_{oc}\)
相当于 \(i = 0\)
时候的电压,称为开路电压;而 \(I_{sc}\) 相当于\(u = 0\)
时候的电流,称为短路电流。根据上述的伏安特性曲线,就可以使用电压源和电阻的串联组合,或者电流源与电导的并联组合,来作为实际电源的电路模型。
注意:上述参数当中的下标 \(_{OC}\) 是开路(Open Circuit)的英文缩写,而下标 \(_{SC}\) 是短路(Short Circuit)的英文缩写。
下图所示为电压源 \(U_s\) 和电阻 \(R\) 的串联组合,此时端子
1 - 1' 位置的电压 \(u\) 与输出电流 \(i\) 的关系为 \(u
= U_s - Ri\):

下图所示为电流源 \(I_s\) 和电导 \(G\) 的并联组合,此时端子
1 - 1' 位置的电压 \(u\) 与输出电流 \(i\) 的关系为 \(i
= I_s - Gu\):
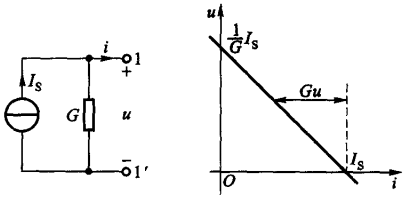
如果使得 \(G = \frac{1}{R}\) 并且
\(I_s = G
U_s\),那么上面两个电压 \(u\) 与输出电流 \(i\) 关系的方程就会完全相同(即端子
1 - 1' 位置的电压 u 与电流 i
的关系完全相同),也就满足了对外等效的必需条件(\(I_s\) 的参考方向是由 \(U_s\)
的负极指向正极)。
注意:当 \(i = 0\) 的时候,端子
1 - 1'位置的电压 \(u\) 为开路电压 \(U_{oc}\)(此时 \(U_{oc} = U_s\)),而当 \(u = 0\) 的时候,电流 \(i\) 等于将端子1 - 1'短路之后的短路电流 \(I_{sc}\)(此时 \(I_{sc} = I_s\)),由此就可以得到 \(U_{oc} = RI_{sc}\) 或者 \(I_{sc} = GU_{oc}\) 的关系。
输入电阻
端口是指电路向外引出的一对端子,可以用于与外部电路进行联结。对于一个端口而言,从其一个端子流入的电流,必然等于从另一个端子流出的电流。这种向外引出一对端子的电路称为一端口网络,其表示符号如下面所示:
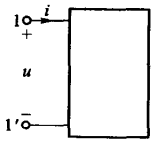
无论一端口网络内部结构如何复杂,其端口电压 \(u\) 总是与端口电流 \(i\) 呈正比,因此可以定义该一端口网络的输入电阻 \(R_i\) 等于:
\[ 输入电阻 R_i = \frac{端口电压\ u}{端口电流\ i} \]
端口的输入电阻本质上就是端口的等效电阻,但是两者在含意上会存在区别。求解端口输入电阻的一般方法称为电压电流法,即在端口添加电压源 \(u_S\),然后根据上述输入电阻公式求解出端口电流 \(i\);或者在端口添加电流源 \(i_S\),然后同样根据输入电阻公式求解出端口电压 \(u\)。
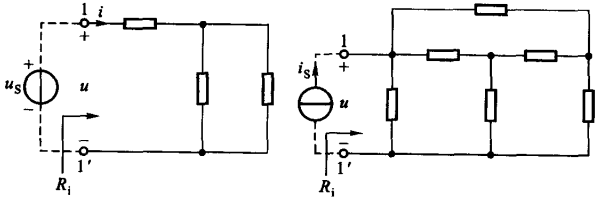
例如上图左侧电路中的一端口网络输入电阻,可以通过电阻的串并联简化求解。而右侧的电路具有桥形结构,则需要运用 \(Y - \Delta\) 变换之后才能够进行简化求解。除此之外,也可以利用电压电流法进行更加方便的求解计算。
电阻电路的一般分析
电路定理
高等教育出版社《电路原理》温习札记




